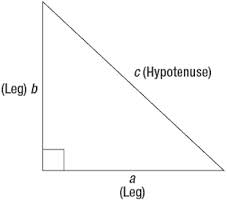
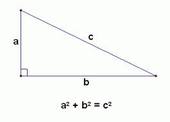
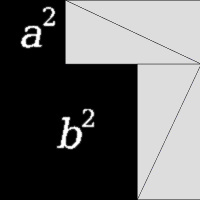
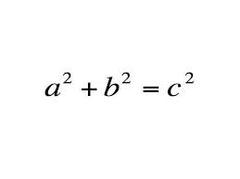Proving the Pythagorean Theorem
Euclid's Proof of the Pythagorean TheoremWatch this video and fill in your notes.
|
Dissecting the Pythagorean TheoremWatch this video then use a piece of paper to duplicate this example.
|
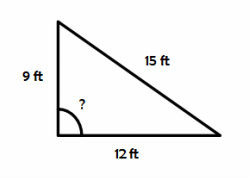
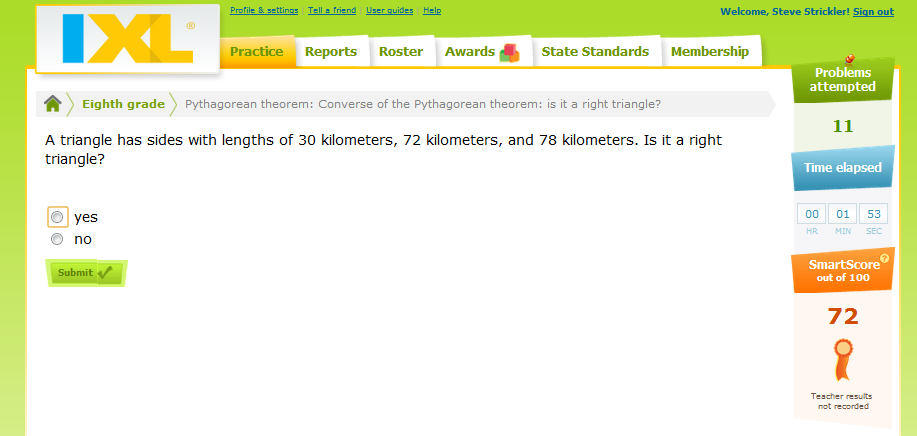
The Converse of the Pythagorean Theorem
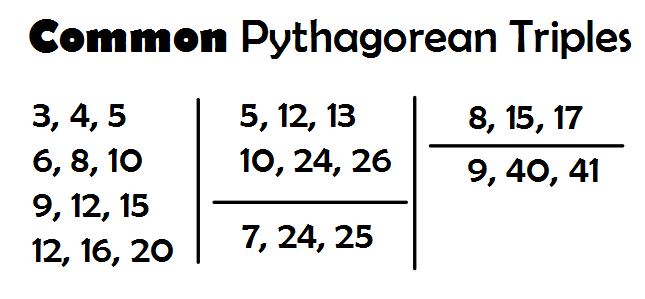
Do the following lengths form right triangles?
|
|
|
|