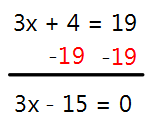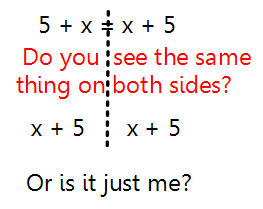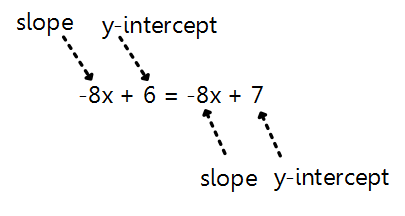7. Solve linear equations in one variable.
A. Give examples of linear equations in one variable with one solution, infinitely many solutions, or no solutions. Show which of these possibilities is the case by successively transforming the given equation into simpler forms, until an equivalent equation of the form x = a, a = a, or a = b results (where a and b are different numbers).
A. Give examples of linear equations in one variable with one solution, infinitely many solutions, or no solutions. Show which of these possibilities is the case by successively transforming the given equation into simpler forms, until an equivalent equation of the form x = a, a = a, or a = b results (where a and b are different numbers).
Lesson: How many solutions?
|
One Solution
|
Infinite Solutions
|
No Solution
|
Check this out!
|
What if we take 3x + 4 = 19 and look at it a different way?
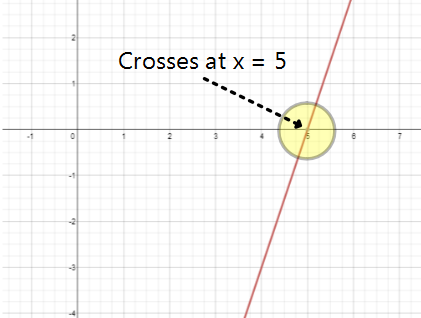
Now, let's pretend that the equation 3x - 15 = 0 is just like what we learned about last unit (y = 3x - 15). Instead of it being equal to zero, we will pretend zero is "y". Let's see what happens when we graph it!
It crosses the x-axis at 5! This means when the y-value is zero that the x-value is 5. If only one "x" exists in the equation (3x + 5 = 19) then there will only be ONE SOLUTION!
|
What if we take a different approach for 5 + x = x + 5?
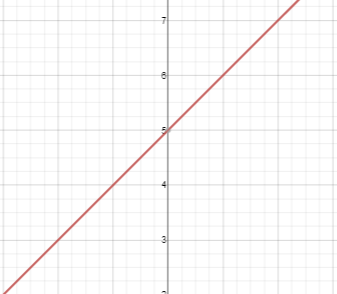
Now, let's pretend that x + 5 is the equation y = x + 5 and graph it on the coordinate plane. Well, actually we will graph it twice. One for each side.
You may not realize this, but we just graphed the same line twice. It is like drawing one line on top of another. The two lines intersect EVERYWHERE! Therefore, there are INFINITE SOLUTIONS!
|
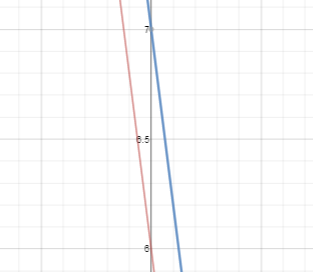
What if we take a different approach for -8x + 6 = -8x + 7?
So, what we are going to do now is graph both sides of the equation as if they were both linear equations of the form "y = mx + b". We will then see where the two lines intersect. The intersection point will give us the answer.
They do not touch! Oh, right...because they have the same slop and start in different places on the y-axis. If the two lines do not intersect, then there is NO SOLUTION!
|